Ellipsoidal Calculus¶
Basic Notions¶
We start with basic definitions.
Definition. Ellipsoid 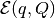 in
in
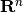 with center
with center 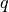 and shape matrix
and shape matrix 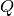 is
the set
is
the set
(1)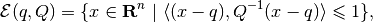
wherein 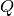 is positive definite (
is positive definite (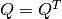 and
and
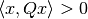 for all nonzero
for all nonzero 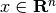 ).
Here
).
Here 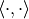 denotes inner
product.
denotes inner
product.
Definition. The support function of a set
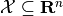 is
is
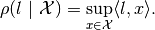
In particular, the support function of the ellipsoid (1) is
(2)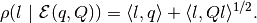
Although in (1) 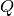 is assumed to be positive definite,
in practice we may deal with situations when
is assumed to be positive definite,
in practice we may deal with situations when 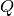 is singular, that
is, with degenerate ellipsoids flat in those directions for which the
corresponding eigenvalues are zero. Therefore, it is useful to give an
alternative definition of an ellipsoid using the expression (2).
is singular, that
is, with degenerate ellipsoids flat in those directions for which the
corresponding eigenvalues are zero. Therefore, it is useful to give an
alternative definition of an ellipsoid using the expression (2).
Definition. Ellipsoid 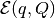 in
in 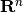 with center
with center
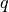 and shape matrix
and shape matrix 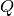 is the set
is the set
(3)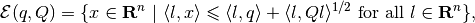
wherein matrix 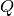 is positive semidefinite (
is positive semidefinite (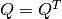 and
and
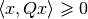 for all
for all 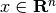 ).
The volume of ellipsoid
).
The volume of ellipsoid 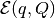 is
is
(4)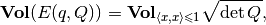
where 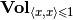 is the volume of
the unit ball in
is the volume of
the unit ball in 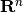 :
:
(5)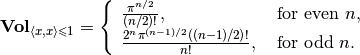
The distance from 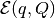 to the fixed point
to the fixed point  is
is
(6)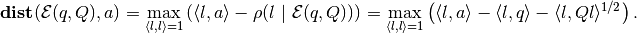
If 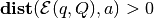 ,
,  lies outside
lies outside
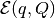 ; if
; if
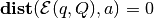 ,
,  is a boundary
point of
is a boundary
point of 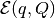 ; if
; if
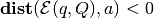 ,
,  is an internal
point of
is an internal
point of 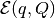 .
.
Given two ellipsoids, 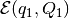 and
and
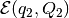 , the distance between them is
, the distance between them is
(7)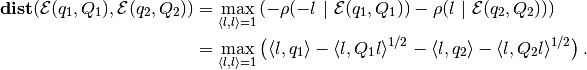
If 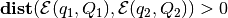 ,
the ellipsoids have no common points; if
,
the ellipsoids have no common points; if
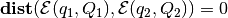 , the
ellipsoids have one common point - they touch; if
, the
ellipsoids have one common point - they touch; if
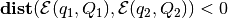 , the
ellipsoids intersect.
, the
ellipsoids intersect.
Finding 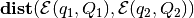 using QCQP is
using QCQP is
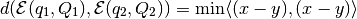
subject to:
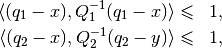
where
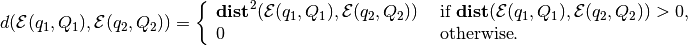
Checking if 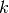 nondegenerate ellipsoids
nondegenerate ellipsoids
 have nonempty
intersection, can be cast as a quadratically constrained quadratic
programming (QCQP) problem:
have nonempty
intersection, can be cast as a quadratically constrained quadratic
programming (QCQP) problem:

subject to:
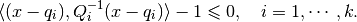
If this problem is feasible, the intersection is nonempty.
Definition. Given compact convex set 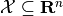 , its polar
set, denoted
, its polar
set, denoted 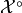 , is
, is
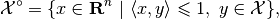
or, equivalently,
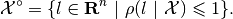
The properties of the polar set are
- If
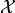 contains the origin,
contains the origin,
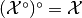 ;
; - If
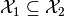 ,
,
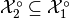 ;
; - For any nonsingular matrix
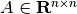 ,
,
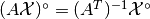 .
.
If a nondegenerate ellipsoid 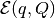 contains the
origin, its polar set is also an ellipsoid:
contains the
origin, its polar set is also an ellipsoid:
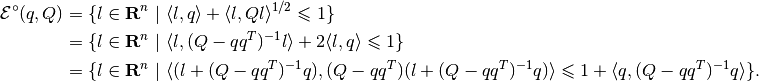
The special case is
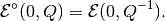
Definition. Given 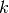 compact sets
compact sets
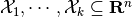 , their
geometric (Minkowski) sum is
, their
geometric (Minkowski) sum is
(8)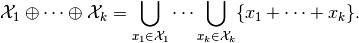
Definition. Given two compact sets
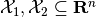 , their
geometric (Minkowski) difference is
, their
geometric (Minkowski) difference is
(9)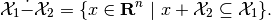
Ellipsoidal calculus concerns the following set of operations:
- affine transformation of ellipsoid;
- geometric sum of finite number of ellipsoids;
- geometric difference of two ellipsoids;
- intersection of finite number of ellipsoids.
These operations occur in reachability calculation and verification of piecewise affine dynamical systems. The result of all of these operations, except for the affine transformation, is not generally an ellipsoid but some convex set, for which we can compute external and internal ellipsoidal approximations.
Additional operations implemented in the Ellipsoidal Toolbox include external and internal approximations of intersections of ellipsoids with hyperplanes, halfspaces and polytopes.
Definition. Hyperplane 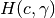 in
in
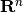 is the set
is the set
(10)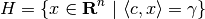
with 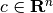 and
and 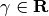 fixed.
The distance from ellipsoid
fixed.
The distance from ellipsoid 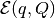 to
hyperplane
to
hyperplane 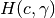 is
is
(11)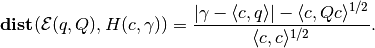
If 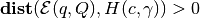 , the ellipsoid
and the hyperplane do not intersect; if
, the ellipsoid
and the hyperplane do not intersect; if
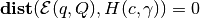 , the hyperplane is a
supporting hyperplane for the ellipsoid; if
, the hyperplane is a
supporting hyperplane for the ellipsoid; if
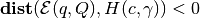 , the ellipsoid
intersects the hyperplane. The intersection of an ellipsoid with a
hyperplane is always an ellipsoid and can be computed directly.
, the ellipsoid
intersects the hyperplane. The intersection of an ellipsoid with a
hyperplane is always an ellipsoid and can be computed directly.
Checking if the intersection of 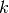 nondegenerate ellipsoids
nondegenerate ellipsoids
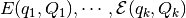 intersects hyperplane
intersects hyperplane
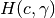 , is equivalent to the feasibility check of the QCQP
problem:
, is equivalent to the feasibility check of the QCQP
problem:

subject to:
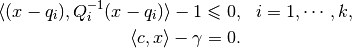
A hyperplane defines two (closed) halfspaces:
(12)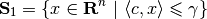
and
(13)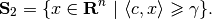
To avoid confusion, however, we shall further assume that a hyperplane
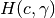 specifies the halfspace in the sense (12).
In order to refer to the other halfspace, the same hyperplane should be
defined as
specifies the halfspace in the sense (12).
In order to refer to the other halfspace, the same hyperplane should be
defined as 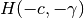 .
.
The idea behind the calculation of intersection of an ellipsoid with a
halfspace is to treat the halfspace as an unbounded ellipsoid, that is,
as the ellipsoid with the shape matrix all but one of whose eigenvalues
are 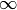 .
.
Definition. Polytope 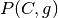 is the
intersection of a finite number of closed halfspaces:
is the
intersection of a finite number of closed halfspaces:
(14)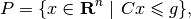
wherein ![C=[c_1 ~ \cdots ~ c_m]^T\in{\bf R}^{m\times n}](_images/math/86f818df7e2b254fc720568f339a1b81c7113d58.png) and
and
![g=[\gamma_1 ~ \cdots ~ \gamma_m]^T\in{\bf R}^m](_images/math/01ca0cd9a8e1fd971cd2fff653566c7037f50d69.png) .
The distance
from ellipsoid
.
The distance
from ellipsoid 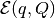 to the polytope
to the polytope 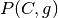 is
is
(15)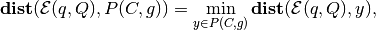
where 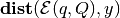 comes from
([dist:sub:point]). If
comes from
([dist:sub:point]). If
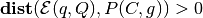 , the ellipsoid and the
polytope do not intersect; if
, the ellipsoid and the
polytope do not intersect; if
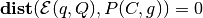 , the ellipsoid touches
the polytope; if
, the ellipsoid touches
the polytope; if 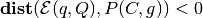 , the
ellipsoid intersects the polytope.
, the
ellipsoid intersects the polytope.
Checking if the intersection of 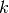 nondegenerate ellipsoids
nondegenerate ellipsoids
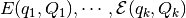 intersects polytope
intersects polytope
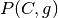 is equivalent to the feasibility check of the QCQP
problem:
is equivalent to the feasibility check of the QCQP
problem:

subject to:

Operations with Ellipsoids¶
Affine Transformation¶
The simplest operation with ellipsoids is an affine transformation. Let
ellipsoid 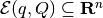 , matrix
, matrix
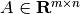 and vector
and vector 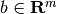 . Then
. Then
(16)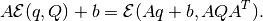
Thus, ellipsoids are preserved under affine transformation. If the rows
of 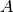 are linearly independent (which implies
are linearly independent (which implies
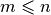 ), and
), and 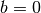 , the affine transformation is
called projection.
, the affine transformation is
called projection.
Geometric Sum¶
Consider the geometric sum (8) in which
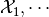 ,
,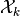 are nondegenerate
ellipsoids
are nondegenerate
ellipsoids 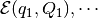 ,
,
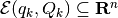 . The resulting set is
not generally an ellipsoid. However, it can be tightly approximated by
the parametrized families of external and internal ellipsoids.
. The resulting set is
not generally an ellipsoid. However, it can be tightly approximated by
the parametrized families of external and internal ellipsoids.
Let parameter 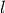 be some nonzero vector in
be some nonzero vector in 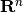 .
Then the external approximation
.
Then the external approximation 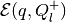 and the
internal approximation
and the
internal approximation 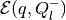 of the sum
of the sum
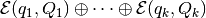 are
tight along direction
are
tight along direction 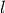 , i.e.,
, i.e.,
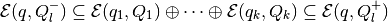
and
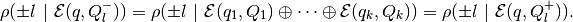
Here the center 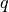 is
is
(17)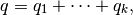
the shape matrix of the external ellipsoid 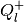 is
is
(18)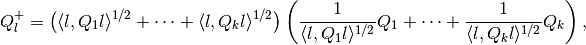
and the shape matrix of the internal ellipsoid 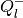 is
is
(19)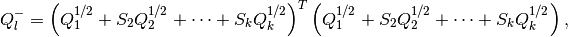
with matrices 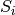 ,
, 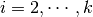 , being orthogonal
(
, being orthogonal
(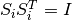 ) and such that vectors
) and such that vectors
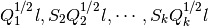 are parallel.
are parallel.
Varying vector 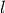 we get exact external and internal
approximations,
we get exact external and internal
approximations,
For proofs of formulas given in this section, see [KUR1997], [KUR2000].
One last comment is about how to find orthogonal matrices
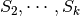 that align vectors
that align vectors
 with
with 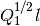 . Let
. Let
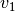 and
and 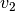 be some unit vectors in
be some unit vectors in 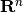 .
We have to find matrix
.
We have to find matrix 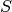 such that
such that
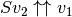 .
We suggest explicit formulas for the
calculation of this matrix [DAR2012]:
.
We suggest explicit formulas for the
calculation of this matrix [DAR2012]:
(20)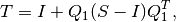
(21)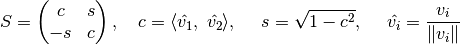
(22)![Q_1 = [q_1 \, q_2]\in \mathbb{R}^{n\times2},\ \quad q_1 = \hat{v_1},\ \quad q_2 = \begin{cases}
s^{-1}(\hat{v_2} - c\hat{v_1}),& s\ne 0\\
0,& s = 0.
\end{cases}](_images/math/0bd74016464a77c91c06d08c1a038bd6d7e46208.png)
Geometric Difference¶
Consider the geometric difference (9) in which the sets
 and
and 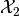 are nondegenerate
ellipsoids
are nondegenerate
ellipsoids 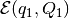 and
and
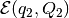 . We say that ellipsoid
. We say that ellipsoid
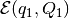 is bigger than ellipsoid
is bigger than ellipsoid
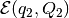 if
if
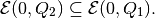
If this condition is not fulfilled, the geometric difference
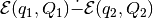 is an empty
set:
is an empty
set:

If 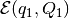 is bigger than
is bigger than
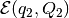 and
and 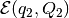 is
bigger than
is
bigger than 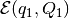 , in other words, if
, in other words, if
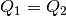 ,
,
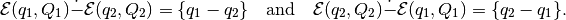
To check if ellipsoid 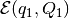 is bigger than
ellipsoid
is bigger than
ellipsoid 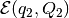 , we perform simultaneous
diagonalization of matrices
, we perform simultaneous
diagonalization of matrices 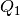 and
and 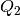 , that is, we
find matrix
, that is, we
find matrix 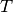 such that
such that
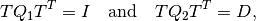
where 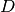 is some diagonal matrix. Simultaneous diagonalization
of
is some diagonal matrix. Simultaneous diagonalization
of 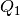 and
and 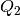 is possible because both are symmetric
positive definite (see [GANT1960]). To find such matrix
is possible because both are symmetric
positive definite (see [GANT1960]). To find such matrix
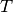 , we first do the SVD of
, we first do the SVD of 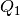 :
:
(23)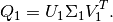
Then the SVD of matrix
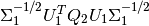 :
:
(24)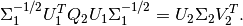
Now, 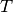 is defined as
is defined as
(25)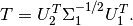
If the biggest diagonal element (eigenvalue) of matrix 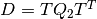 is less than or equal to
is less than or equal to 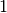 ,
,
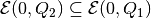 .
.
Once it is established that ellipsoid 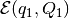 is
bigger than ellipsoid
is
bigger than ellipsoid 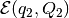 , we know that their
geometric difference
, we know that their
geometric difference
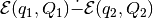 is a nonempty
convex compact set. Although it is not generally an ellipsoid, we can
find tight external and internal approximations of this set parametrized
by vector
is a nonempty
convex compact set. Although it is not generally an ellipsoid, we can
find tight external and internal approximations of this set parametrized
by vector 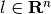 . Unlike geometric sum, however,
ellipsoidal approximations for the geometric difference do not exist for
every direction
. Unlike geometric sum, however,
ellipsoidal approximations for the geometric difference do not exist for
every direction 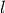 . Vectors for which the approximations do not
exist are called bad directions.
. Vectors for which the approximations do not
exist are called bad directions.
Given two ellipsoids 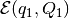 and
and
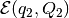 with
with
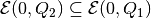 ,
, 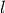 is a
bad direction if
is a
bad direction if
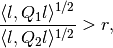
in which  is a minimal root of the equation
is a minimal root of the equation
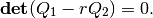
To find  , compute matrix
, compute matrix 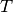 by (23)-(25)
and define
by (23)-(25)
and define
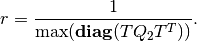
If 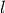 is not a bad direction, we can find tight external and
internal ellipsoidal approximations
is not a bad direction, we can find tight external and
internal ellipsoidal approximations 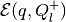 and
and
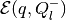 such that
such that
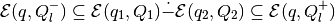
and
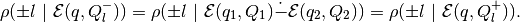
The center 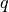 is
is
(26)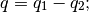
the shape matrix of the internal ellipsoid 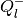 is
is
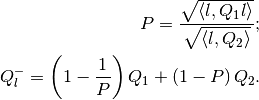
and the shape matrix of the external ellipsoid 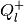 is
is
(27)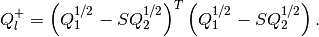
Here 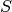 is an orthogonal matrix such that vectors
is an orthogonal matrix such that vectors
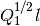 and
and 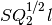 are parallel.
are parallel. 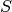 is
found from (20)-(22), with
is
found from (20)-(22), with 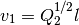 and
and
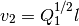 .
.
Running 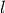 over all unit directions that are not bad, we get
over all unit directions that are not bad, we get
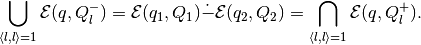
For proofs of formulas given in this section, see [KUR1997].
Geometric Difference-Sum¶
Given ellipsoids 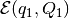 ,
,
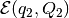 and
and 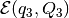 , it is
possible to compute families of external and internal approximating
ellipsoids for
, it is
possible to compute families of external and internal approximating
ellipsoids for
(28)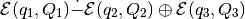
parametrized by direction 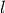 , if this set is nonempty
(
, if this set is nonempty
(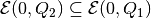 ).
).
First, using the result of the previous section, for any direction
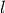 that is not bad, we obtain tight external
that is not bad, we obtain tight external
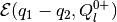 and internal
and internal
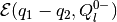 approximations of the set
approximations of the set
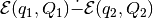 .
.
The second and last step is, using the result of section 2.2.2, to find
tight external ellipsoidal approximation
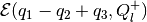 of the sum
of the sum
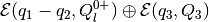 , and
tight internal ellipsoidal approximation
, and
tight internal ellipsoidal approximation
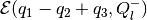 for the sum
for the sum
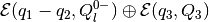 .
.
As a result, we get
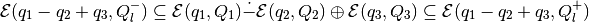
and
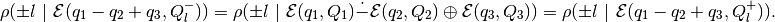
Running 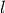 over all unit vectors that are not bad, this
translates to
over all unit vectors that are not bad, this
translates to
Geometric Sum-Difference¶
Given ellipsoids 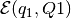 ,
,
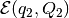 and
and 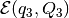 , it is
possible to compute families of external and internal approximating
ellipsoids for
, it is
possible to compute families of external and internal approximating
ellipsoids for
(29)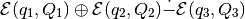
parametrized by direction 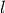 , if this set is nonempty
(
, if this set is nonempty
(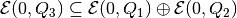 ).
).
First, using the result of section 2.2.2, we obtain tight external
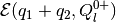 and internal
and internal
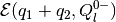 ellipsoidal approximations of the
set
ellipsoidal approximations of the
set 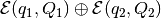 . In order
for the set (29) to be nonempty, inclusion
. In order
for the set (29) to be nonempty, inclusion
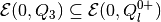 must be
true for any
must be
true for any 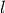 . Note, however, that even if (29) is
nonempty, it may be that
. Note, however, that even if (29) is
nonempty, it may be that
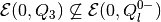 , then
internal approximation for this direction does not exist.
, then
internal approximation for this direction does not exist.
Assuming that (29) is nonempty and
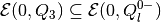 , the second
step would be, using the results of section 2.2.3, to compute tight
external ellipsoidal approximation
, the second
step would be, using the results of section 2.2.3, to compute tight
external ellipsoidal approximation
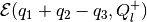 of the difference
of the difference
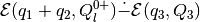 ,
which exists only if
,
which exists only if 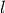 is not bad, and tight internal
ellipsoidal approximation
is not bad, and tight internal
ellipsoidal approximation 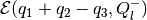 of the
difference
of the
difference
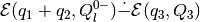 ,
which exists only if
,
which exists only if 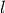 is not bad for this difference.
is not bad for this difference.
If approximation 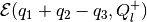 exists, then
exists, then
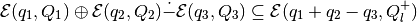
and
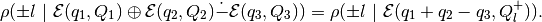
If approximation 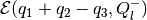 exists, then
exists, then
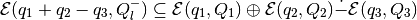
and
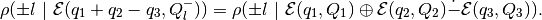
For any fixed direction 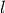 it may be the case that neither
external nor internal tight ellipsoidal approximations exist.
it may be the case that neither
external nor internal tight ellipsoidal approximations exist.
Intersection of Ellipsoid and Hyperplane¶
Let nondegenerate ellipsoid 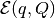 and hyperplane
and hyperplane
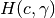 be such that
be such that
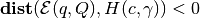 . In other words,
. In other words,
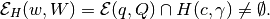
The intersection of ellipsoid with hyperplane, if nonempty, is always an ellipsoid. Here we show how to find it.
First of all, we transform the hyperplane 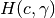 into
into
![H([1~0~\cdots~0]^T, 0)](_images/math/ae2329fc5b2fffd5e099ee1533b1b8095cd2f6eb.png) by the affine transformation
by the affine transformation
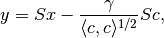
where 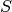 is an orthogonal matrix found by (20)-(22)
with
is an orthogonal matrix found by (20)-(22)
with 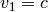 and
and ![v_2=[1~0~\cdots~0]^T](_images/math/cd79adafa969dbc6073abfe662255885da4e26f5.png) . The ellipsoid in
the new coordinates becomes
. The ellipsoid in
the new coordinates becomes 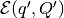 with
with
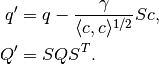
Define matrix 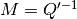 ;
; 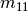 is its element in
position
is its element in
position 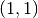 ,
, 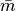 is the first column of
is the first column of 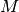 without the first element, and
without the first element, and 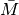 is the submatrix of
is the submatrix of
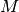 obtained by stripping
obtained by stripping 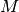 of its first row and first
column:
of its first row and first
column:
![M = \left[\begin{array}{c|cl}
m_{11} & & \bar{m}^T\\
& \\
\hline
& \\
\bar{m} & & \bar{M}\end{array}\right].](_images/math/981e90dfe6eae9e2420bffe5b152be7e7bde3173.png)
The ellipsoid resulting from the intersection is
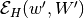 with
with
![\begin{aligned}
w' & = q' + q_1'\left[\begin{array}{c}
-1\\
\bar{M}^{-1}\bar{m}\end{array}\right],\\
W' & = \left(1-q_1'^2(m_{11}-
\langle\bar{m},\bar{M}^{-1}\bar{m}\rangle)\right)\left[\begin{array}{c|cl}
0 & & {\bf 0}\\
& \\
\hline
& \\
{\bf 0} & & \bar{M}^{-1}\end{array}\right],\end{aligned}](_images/math/139c7174816a0c690a86fb833d28f0c0c73e3ea5.png)
in which 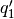 represents the first element of vector
represents the first element of vector 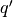 .
.
Finally, it remains to do the inverse transform of the coordinates to
obtain ellipsoid 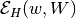 :
:
Intersection of Ellipsoid and Ellipsoid¶
Given two nondegenerate ellipsoids 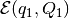 and
and
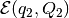 ,
,
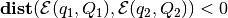 implies that
implies that
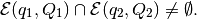
This intersection can be approximated by ellipsoids from the outside
and from the inside. Trivially, both 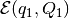 and
and
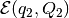 are external approximations of this
intersection. Here, however, we show how to find the external
ellipsoidal approximation of minimal volume.
are external approximations of this
intersection. Here, however, we show how to find the external
ellipsoidal approximation of minimal volume.
Define matrices

Minimal volume external ellipsoidal approximation
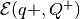 of the intersection
of the intersection
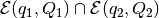 is determined
from the set of equations:
is determined
from the set of equations:
(30)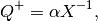
(31)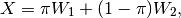
(32)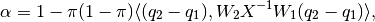
(33)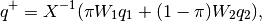
(34)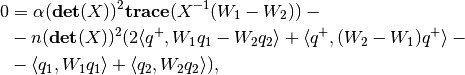
with 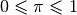 . We substitute
. We substitute 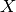 ,
,
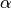 ,
, 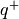 defined in (31)-(33) into
(34) and get a polynomial of degree
defined in (31)-(33) into
(34) and get a polynomial of degree 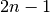 with respect to
with respect to
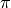 , which has only one root in the interval
, which has only one root in the interval ![[0,1]](_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) ,
,
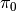 . Then, substituting
. Then, substituting 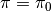 into
(30)-(33), we obtain
into
(30)-(33), we obtain 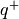 and
and 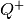 . Special
cases are
. Special
cases are 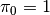 , whence
, whence
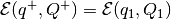 , and
, and
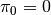 , whence
, whence
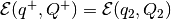 . These situations
may occur if, for example, one ellipsoid is contained in the other:
. These situations
may occur if, for example, one ellipsoid is contained in the other:
The proof that the system of equations (30)-(34) correctly
defines the minimal volume external ellipsoidal approximationi of the
intersection 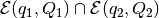 is
given in [ROS2002].
is
given in [ROS2002].
To find the internal approximating ellipsoid
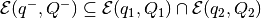 ,
define
,
define
(35)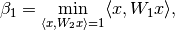
(36)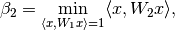
Notice that (35) and (36) are QCQP problems. Parameters
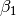 and
and 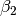 are invariant with respect to affine
coordinate transformation and describe the position of ellipsoids
are invariant with respect to affine
coordinate transformation and describe the position of ellipsoids
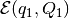 ,
, 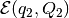 with
respect to each other:
with
respect to each other:
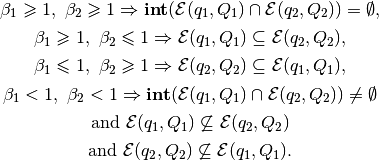
Define parametrized family of internal ellipsoids
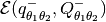 with
with
(37)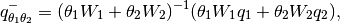
(38)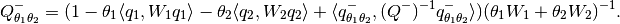
The best internal ellipsoid
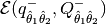 in the class (37)-(38), namely, such that
in the class (37)-(38), namely, such that
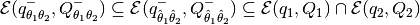
for all 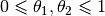 , is specified by
the parameters
, is specified by
the parameters
(39)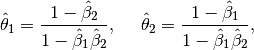
with

It is the ellipsoid that we look for:
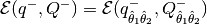 .
Two special cases are
.
Two special cases are
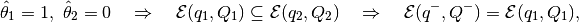
and
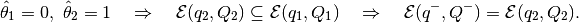
The method of finding the internal ellipsoidal approximation of the intersection of two ellipsoids is described in [VAZ1999].
Intersection of Ellipsoid and Halfspace¶
Finding the intersection of ellipsoid and halfspace can be reduced to
finding the intersection of two ellipsoids, one of which is unbounded.
Let 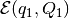 be a nondegenerate ellipsoid and let
be a nondegenerate ellipsoid and let
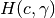 define the halfspace
define the halfspace
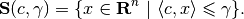
We have to determine if the intersection
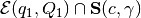 is empty, and if not,
find its external and internal ellipsoidal approximations,
is empty, and if not,
find its external and internal ellipsoidal approximations,
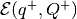 and
and 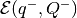 . Two
trivial situations are:
. Two
trivial situations are:
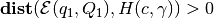 and
and
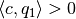 , which implies that
, which implies that
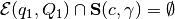 ;
;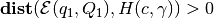 and
and
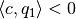 , so that
, so that
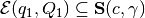 , and then
, and then
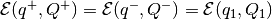 .
.
In case 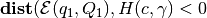 , i.e. the
ellipsoid intersects the hyperplane,
, i.e. the
ellipsoid intersects the hyperplane,
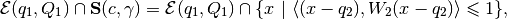
with
(40)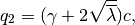
(41)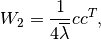
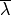 being the biggest eigenvalue of matrix
being the biggest eigenvalue of matrix
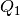 . After defining
. After defining 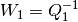 , we obtain
, we obtain
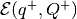 from equations (30)-(34), and
from equations (30)-(34), and
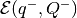 from (37)-(38),
(39).
from (37)-(38),
(39).
Remark. Notice that matrix 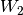 has rank
has rank 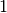 , which
makes it singular for
, which
makes it singular for 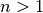 . Nevertheless, expressions
(30)-(31), (37)-(38) make sense because
. Nevertheless, expressions
(30)-(31), (37)-(38) make sense because
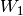 is nonsingular,
is nonsingular, 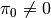 and
and
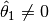 .
.
To find the ellipsoidal approximations 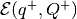 and
and
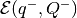 of the intersection of ellipsoid
of the intersection of ellipsoid
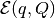 and polytope
and polytope 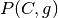 ,
,
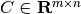 ,
, 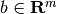 , such that
, such that
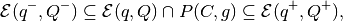
we first compute
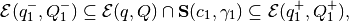
wherein 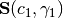 is the halfspace defined by the
first row of matrix
is the halfspace defined by the
first row of matrix  ,
, 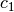 , and the first element of
vector
, and the first element of
vector 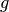 ,
, 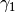 . Then, one by one, we get
. Then, one by one, we get
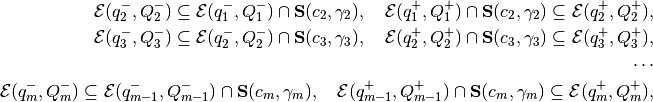
The resulting ellipsoidal approximations are

Checking if one ellipsoid contains another¶
Theorem of alternatives, also known as 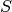 -procedure [BOYD2004],
states that the implication
-procedure [BOYD2004],
states that the implication
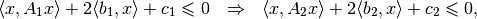
where 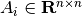 are symmetric matrices,
are symmetric matrices,
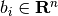 ,
, 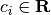 ,
, 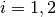 , holds if
and only if there exists
, holds if
and only if there exists 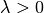 such that
such that
![\left[\begin{array}{cc}
A_2 & b_2\\
b_2^T & c_2\end{array}\right]
\preceq
\lambda\left[\begin{array}{cc}
A_1 & b_1\\
b_1^T & c_1\end{array}\right].](_images/math/bad3773668070eab0a4ef0bf7572ed7f7635efb3.png)
By 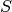 -procedure,
-procedure,
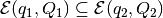 (both
ellipsoids are assumed to be nondegenerate) if and only if the following
SDP problem is feasible:
(both
ellipsoids are assumed to be nondegenerate) if and only if the following
SDP problem is feasible:

subject to:
![\begin{aligned}
\lambda & > 0, \\
\left[\begin{array}{cc}
Q_2^{-1} & -Q_2^{-1}q_2\\
(-Q_2^{-1}q_2)^T & q_2^TQ_2^{-1}q_2-1\end{array}\right]
& \preceq
\lambda \left[\begin{array}{cc}
Q_1^{-1} & -Q_1^{-1}q_1\\
(-Q_1^{-1}q_1)^T & q_1^TQ_1^{-1}q_1-1\end{array}\right]\end{aligned}](_images/math/57166a2606512f8eaddb8414e9f6327cae1c6e12.png)
where 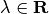 is the variable.
is the variable.
Minimum Volume Ellipsoids¶
The minimum volume ellipsoid that contains set 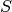 is called
Löwner-John ellipsoid of the set
is called
Löwner-John ellipsoid of the set 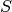 . To characterize it we
rewrite general ellipsoid
. To characterize it we
rewrite general ellipsoid 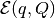 as
as
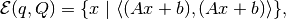
where
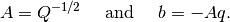
For positive definite matrix 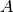 , the volume of
, the volume of
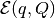 is proportional to
is proportional to 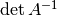 . So,
finding the minimum volume ellipsoid containing
. So,
finding the minimum volume ellipsoid containing 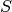 can be
expressed as semidefinite programming (SDP) problem
can be
expressed as semidefinite programming (SDP) problem
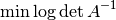
subject to:
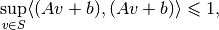
where the variables are 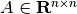 and
and
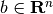 , and there is an implicit constraint
, and there is an implicit constraint
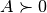 (
(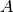 is positive definite). The objective and
constraint functions are both convex in
is positive definite). The objective and
constraint functions are both convex in 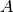 and
and 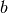 , so this
problem is convex. Evaluating the constraint function, however, requires
solving a convex maximization problem, and is tractable only in certain
special cases.
, so this
problem is convex. Evaluating the constraint function, however, requires
solving a convex maximization problem, and is tractable only in certain
special cases.
For a finite set 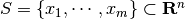 , an
ellipsoid covers
, an
ellipsoid covers 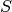 if and only if it covers its convex hull. So,
finding the minimum volume ellipsoid covering
if and only if it covers its convex hull. So,
finding the minimum volume ellipsoid covering 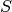 is the same as
finding the minimum volume ellipsoid containing the polytope
is the same as
finding the minimum volume ellipsoid containing the polytope
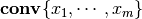 . The SDP problem is
. The SDP problem is
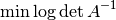
subject to:
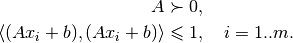
We can find the minimum volume ellipsoid containing the union of
ellipsoids 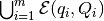 . Using the fact
that for
. Using the fact
that for 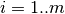
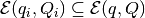 if and only if
there exists
if and only if
there exists 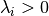 such that
such that
![\left[\begin{array}{cc}
A^2 - \lambda_i Q_i^{-1} & Ab + \lambda_i Q_i^{-1}q_i\\
(Ab + \lambda_i Q_i^{-1}q_i)^T & b^Tb-1 - \lambda_i (q_i^TQ_i^{-1}q_i-1) \end{array}
\right] \preceq 0 .](_images/math/22e24c1e3cbef4e8501089bc30d0ab22023c9095.png)
Changing variable 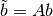 , we get convex SDP in the
variables
, we get convex SDP in the
variables 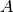 ,
, 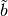 , and
, and
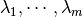 :
:
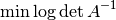
subject to:
![\begin{aligned}
\lambda_i & > 0,\\
\left[\begin{array}{ccc}
A^2-\lambda_iQ_i^{-1} & \tilde{b}+\lambda_iQ_i^{-1}q_i & 0 \\
(\tilde{b}+\lambda_iQ_i^{-1}q_i)^T & -1-\lambda_i(q_i^TQ_i^{-1}q_i-1) & \tilde{b}^T \\
0 & \tilde{b} & -A^2\end{array}\right] & \preceq 0, ~~~ i=1..m.\end{aligned}](_images/math/8b3eccef8d2149a781cb3c3453ef67dccefc923f.png)
After 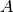 and
and 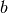 are found,
are found,
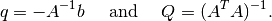
The results on the minimum volume ellipsoids are explained and proven in [BOYD2004].
Maximum Volume Ellipsoids¶
Consider a problem of finding the maximum volume ellipsoid that lies
inside a bounded convex set 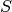 with nonempty interior. To
formulate this problem we rewrite general ellipsoid
with nonempty interior. To
formulate this problem we rewrite general ellipsoid
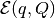 as
as
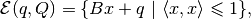
where 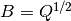 , so the volume of
, so the volume of 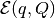 is
proportional to
is
proportional to 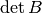 .
.
The maximum volume ellipsoid that lies inside 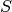 can be found by
solving the following SDP problem:
can be found by
solving the following SDP problem:
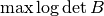
subject to:
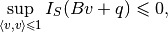
in the variables 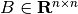 - symmetric matrix,
and
- symmetric matrix,
and 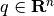 , with implicit constraint
, with implicit constraint 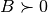 ,
where
,
where 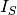 is the indicator function:
is the indicator function:
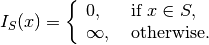
In case of polytope, 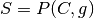 with
with 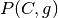 defined in
(14), the SDP has the form
defined in
(14), the SDP has the form
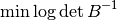
subject to:
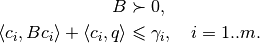
We can find the maximum volume ellipsoid that lies inside the
intersection of given ellipsoids
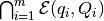 . Using the fact that for
. Using the fact that for
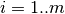
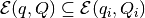 if and only if there exists
if and only if there exists 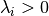 such that
such that
![\left[\begin{array}{cc}
-\lambda_i - q^TQ_i^{-1}q + 2q_i^TQ_i^{-1}q - q_i^TQ_i^{-1}q_i + 1 & (Q_i^{-1}q-Q_i^{-1}q_i)^TB\\
B(Q_i^{-1}q-Q_i^{-1}q_i) & \lambda_iI-BQ_i^{-1}B\end{array}\right] \succeq 0.](_images/math/a9c4516e2736162b6a267628d74c85f4f38974f4.png)
To find the maximum volume ellipsoid, we solve convex SDP in variables
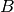 ,
, 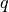 , and
, and 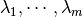 :
:
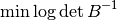
subject to:
![\begin{aligned}
\lambda_i & > 0, \\
\left[\begin{array}{ccc}
1-\lambda_i & 0 & (q - q_i)^T\\
0 & \lambda_iI & B\\
q - q_i & B & Q_i\end{array}\right] & \succeq 0, ~~~ i=1..m.\end{aligned}](_images/math/7b628a9fa6973eb94d1f9730b9ccf6d67d5d38f5.png)
After 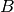 and
and 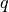 are found,
are found,
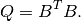
The results on the maximum volume ellipsoids are explained and proven in [BOYD2004].
References
| [DAR2012] | A. N. Dariyn and A. B. Kurzhanski. Method of invariant sets for linear systems of high dimensionality under uncertain disturbances. Doklady Akademii Nauk, 446(6):607–611, 2012. |
| [GANT1960] |
|
| [ROS2002] | F. Thomas L. Ros, A. Sabater. An Ellipsoidal Calculus Based on Propagation and Fusion. IEEE Transactions on Systems, Man and Cybernetics, Part B: Cybernetics, 32(4), 2002. |
| [VAZ1999] | A. Yu. Vazhentsev. On Internal Ellipsoidal Approximations for Problems of Control and Synthesis with Bounded Coordinates. Izvestiya Rossiiskoi Akademii Nauk. Teoriya i Systemi Upravleniya., 1999. |
| [BOYD2004] | (1, 2, 3)
|